XieNaoban's Blog
0%

Codeforces Round 420(Div. 2) - D. Okabe and City

发表于 更新于 分类于 ， 阅读次数： 评论次数：
本文字数： 4.4k 阅读时长 ≈ 4 分钟

Description

Okabe likes to be able to walk through his city on a path lit by street lamps. That way, he doesn't get beaten up by schoolchildren.

Okabe's city is represented by a 2D grid of cells. Rows are numbered from 1 to n from top to bottom, and columns are numbered 1 to mfrom left to right. Exactly k cells in the city are lit by a street lamp. It's guaranteed that the top-left cell is lit.

Okabe starts his walk from the top-left cell, and wants to reach the bottom-right cell. Of course, Okabe will only walk on lit cells, and he can only move to adjacent cells in the up, down, left, and right directions. However, Okabe can also temporarily light all the cells in any single row or column at a time if he pays 1 coin, allowing him to walk through some cells not lit initially.

Note that Okabe can only light a single row or column at a time, and has to pay a coin every time he lights a new row or column. To change the row or column that is temporarily lit, he must stand at a cell that is lit initially. Also, once he removes his temporary light from a row or column, all cells in that row/column not initially lit are now not lit.

Help Okabe find the minimum number of coins he needs to pay to complete his walk!

Input

The first line of input contains three space-separated integers n, m, and k (2 ≤ n, m, k ≤ 104).

Each of the next k lines contains two space-separated integers r i and c i (1 ≤ r i ≤ n, 1 ≤ c i ≤ m) — the row and the column of the i-th lit cell.

It is guaranteed that all k lit cells are distinct. It is guaranteed that the top-left cell is lit.

Output

Print the minimum number of coins Okabe needs to pay to complete his walk, or -1 if it's not possible.

Examples

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
input
4 4 5
1 1
2 1
2 3
3 3
4 3
output
2
input
5 5 4
1 1
2 1
3 1
3 2
output
-1
input
2 2 4
1 1
1 2
2 1
2 2
output
0
input
5 5 4
1 1
2 2
3 3
4 4
output
3

Note

In the first sample test, Okabe can take the path 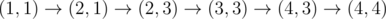img, paying only when moving to (2, 3) and (4, 4).

In the fourth sample, Okabe can take the path 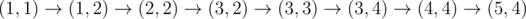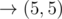img img, paying when moving to (1, 2), (3, 4), and (5, 4).

Key

看了好多题解终于写了出来。。。 题意：\(n \times m\)的图中有\(k\)个点，若某每个点周围四个方向有点，则可耗费0代价到达，若某点的周围的上下五行（向上两行，向下两行，当前行）、左右五列也有点，则可耗费1代价到达。求从左上角到右下角的最短路径。

以\(k\)个点建图，可以看见由于和周围5行5列的点均有边，边非常多，所以不能直接连边。在运行时枚举所有周围的点即可。本质上就是一张无负权边的图，用Dijkstra跑即可。

右下角的点\((n,m)\)可能不在\(k\)个结点里，有点难处理，但思路是赋予它一个结点。一开始我跟着一个题解的思路做，他是把右下角的点赋值一个1。还是挺烦的。后来看到一个高级的：若\((n,m)\)不是\(k\)点中之一，则\(++n\)，\(++m\)，再把\((n,m)\)加入为\(k+1\)个点。很巧妙啊。

不要试图开二维数组，哪怕是开了个\(bool vis[10000][10000]\)，也会在第36个案例MLE。一开始不懂，感觉应该不要紧，因为在本地没什么问题。。。结果为此疯狂WA。

既然不能开二维数组，就只能给每个点编号了，于是一共开了三个类，越写越乱。。。也想过用哈希，但对此不是很熟练，不敢写。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#define INF 0x3f3f3f3f
#define mset(a, b) memset(a,b,sizeof(a))
#define abs(a) ((a)>0?(a):-(a))
using namespace std;
const int maxn = (unsigned)1e4 + 10;
struct Point {
	int r, c, d;
	bool v;
	bool operator <(const Point &p) const {
		if (r == p.r) return c < p.c;
		return r < p.r;
	}
}P[maxn];

struct Node {
	int rc, id;
};
struct QNode {
	int d, id;
	QNode(int _d, int _id) :d(_d), id(_id) {}
	bool operator <(const QNode & p) const {
		return d > p.d;
	}
};
int n, m, k;
vector<Node> R[maxn], C[maxn];

int main()
{
	ios::sync_with_stdio(false);
	cin >> n >> m >> k;
	bool flg = true;
	for (int i = 0; i < k; ++i) {
		auto &now = P[i];
		now.d = INF; now.v = false;
		cin >> now.r >> now.c;
		if (now.r == n&&now.c == m) {
			flg = false;
		}
	}
	if (flg) {
		auto &now = P[k];
		now.r = ++n;
		now.c = ++m;
		now.d = INF;
		now.v = false;
		++k;
	}
	sort(P, P + k);
	Node nod;
	for (int i = 0; i < k; ++i) {
		auto &now = P[i];
		nod.id = i;
		nod.rc = now.c;
		R[now.r].push_back(nod);
		nod.rc = now.r;
		C[now.c].push_back(nod);
	}
	priority_queue<QNode> que;
	P[0].d = 0;
	que.push(QNode(0, 0));
	while (!que.empty()) {
		auto &now = P[que.top().id];
		que.pop();
		if (now.v) continue;
		now.v = true;
		if (now.r == n&&now.c == m) {
			cout << now.d;
			return 0;
		}
		for (int i = -2; i <= 2; ++i) {
			int r = now.r + i;
			if (r >= 1 && r <= n) for (const auto& c : R[r]) {
				if (abs(i) == 1 && c.rc == now.c) {
					if (now.d < P[c.id].d) {
						P[c.id].d = now.d;
						que.push(QNode(P[c.id].d, c.id));
					}
				}
				else if (now.d + 1 < P[c.id].d) {
					P[c.id].d = now.d + 1;
					que.push(QNode(P[c.id].d, c.id));
				}
			}

			int c = now.c + i;
			if (c >= 1 && c <= m) for (const auto& r : C[c]) {
				if (abs(i) == 1 && r.rc == now.r) {
					if (now.d < P[r.id].d) {
						P[r.id].d = now.d;
						que.push(QNode(P[r.id].d, r.id));
					}
				}
				else if (now.d + 1 < P[r.id].d) {
					P[r.id].d = now.d + 1;
					que.push(QNode(P[r.id].d, r.id));
				}
			}
		}
	}
	cout << -1;
	return 0;
}