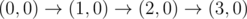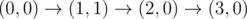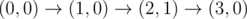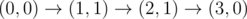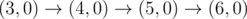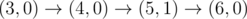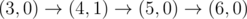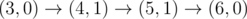Description

Okabe likes to take walks but knows that spies from the Organization could be anywhere; that's why he wants to know how many different walks he can take in his city safely. Okabe's city can be represented as all points (x, y) such that x and y are non-negative. Okabe starts at the origin (point (0, 0)), and needs to reach the point (k, 0). If Okabe is currently at the point (x, y), in one step he can go to (x + 1, y + 1), (x + 1, y), or (x + 1, y - 1).

Additionally, there are n horizontal line segments, the i-th of which goes from x = a i to x = b i inclusive, and is at y = c i. It is guaranteed that a1 = 0, a n ≤ k ≤ b n, and a i = b i - 1 for 2 ≤ i ≤ n. The i-th line segment forces Okabe to walk with y-value in the range 0 ≤ y ≤ c i when his x value satisfies a i ≤ x ≤ b i, or else he might be spied on. This also means he is required to be under two line segments when one segment ends and another begins.

Okabe now wants to know how many walks there are from the origin to the point (k, 0) satisfying these conditions, modulo 109 + 7.

Input

The first line of input contains the integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of segments and the destination x coordinate.

The next n lines contain three space-separated integers a i, b i, and c i (0 ≤ a i < b i ≤ 1018, 0 ≤ c i ≤ 15) — the left and right ends of a segment, and its y coordinate.

It is guaranteed that a1 = 0, a n ≤ k ≤ b n, and a i = b i - 1 for 2 ≤ i ≤ n.

Output

Print the number of walks satisfying the conditions, modulo 1000000007 (109 + 7).

Examples

input
1 3
0 3 3
output
4
input
2 6
0 3 0
3 10 2
output
4

Note

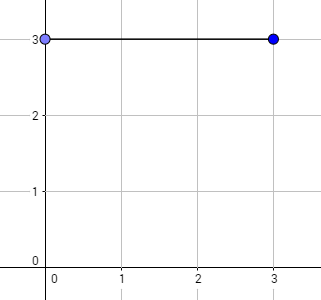
The graph above corresponds to sample 1. The possible walks are:

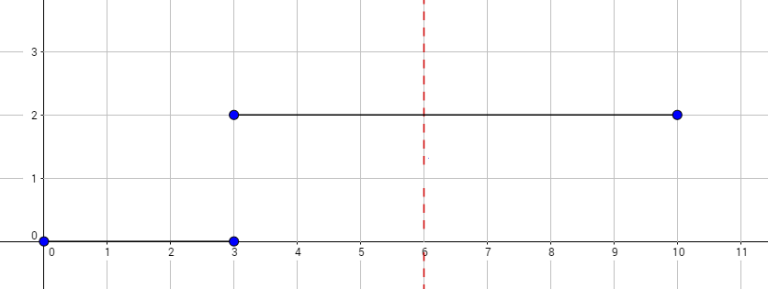
The graph above corresponds to sample 2. There is only one walk for Okabe to reach (3, 0). After this, the possible walks are:

Key

看了题解才知道矩阵快速幂是这么用的。。。用了之后才知道原来这么简单。。

首先每个点只能向3个方向向右行动，明显的DP问题。一步步dp肯定不行，要走18次方步呢。使用矩阵快速幂可以针对每一个段计算，一共就最多一百个段。每个段中，每一步将上一步的结果乘以如下矩阵： \[ \left[ \begin{matrix} 1 & 1 & 0 & 0 & ...\\ 1 & 1 & 1 & 0 & ...\\ 0 & 1 & 1 & 1 & ...\\ 0 & 0 & 1 & 1 & ...\\ ... & ... & ... & ... \end{matrix} \right] \] 就得到这一步的dp答案。一个段有\(b_i-a_i\)次dp，即进行\(b_i-a_i\)次幂。

边界处也好处理，若\(c_{i+1}<c_{i}\)，就直接取dp数组的低\(c_{i}\)位结果即可；若\(c_{i+1}>c_{i}\)，dp数组\(c_{i+1}\)以上的高位补0即可。

Code

#include<iostream>
#include<cstring>
using namespace std;

typedef long long LL;
const int Maxn = 17;
const int Pr = 1e9 + 7;
struct Matrix {
	LL n, m;
	LL mat[Maxn][Maxn];

	Matrix() = default;
	Matrix(LL _n, LL _m) :n(_n), m(_m) {}

	void Clear() {
		memset(mat, 0, sizeof(mat));
	}

	Matrix operator +(const Matrix &M) const {
		Matrix res(n, m);
		for (LL i = 0; i < n; ++i) for (LL j = 0; j < m; ++j) {
			res.mat[i][j] = (mat[i][j] + M.mat[i][j]) % Pr;
		}
		return res;
	}

	Matrix operator *(const Matrix &M) const {
		if (m != M.n) return Matrix(-1, -1);
		Matrix res(n, M.m);
		res.Clear();
		for (LL i = 0; i < n; ++i) for (LL j = 0; j < M.m; ++j) {
			for (LL k = 0; k < m; ++k) {
				res.mat[i][j] += mat[i][k] * M.mat[k][j];
				res.mat[i][j] %= Pr;
			}
		}
		return res;
	}

	Matrix operator ^(LL b) const {
		if (n != m) return Matrix(-1, -1);
		Matrix a(*this);
		Matrix res(n, n);
		res.Clear();
		for (LL i = 0; i < n; ++i) res.mat[i][i] = 1;
		for (; b; b >>= 1) {
			if (b & 1) {
				res = a*res;
			}
			a = a*a;
		}
		return res;
	}

	void Print() {
		for (int i = 0; i < n; ++i) {
			for (int j = 0; j < m; ++j)
				cout << mat[i][j] << ' ';
			cout << '\n';
		}
	}
};

LL N, K;

int main()
{
	ios::sync_with_stdio(false);
	cin >> N >> K;
	Matrix pwr(Maxn, Maxn);
	pwr.Clear();
	for (int i = 0; i < Maxn; ++i) {
		pwr.mat[i][i] = 1;
		if (i > 0) pwr.mat[i][i - 1] = 1;
		if (i + 1 < Maxn) pwr.mat[i][i + 1] = 1;
	}
	Matrix dp(Maxn, 1);
	dp.Clear();
	dp.mat[0][0] = 1;

	LL a, b, c;
	while (N--) {
		cin >> a >> b >> c;
		++c;
		if (b > K) b = K;
		for (int i = dp.n; i < Maxn; ++i)
			dp.mat[i][0] = 0;
		dp.n = c;
		pwr.n = pwr.m = c;
		dp = (pwr ^ (b - a)) * dp;
	}
	cout << dp.mat[0][0];
	return 0;
}

XieNaoban's Blog

Codeforces Round 420(Div. 2) - E. Okabe and El Psy Kongroo