XieNaoban's Blog
0%

Codeforces Round 425(Div. 2) - D. Misha, Grisha and Underground

发表于 更新于 分类于 ， 阅读次数： 评论次数：
本文字数： 3.8k 阅读时长 ≈ 3 分钟

Description

Misha and Grisha are funny boys, so they like to use new underground. The underground has n stations connected with n - 1 routes so that each route connects two stations, and it is possible to reach every station from any other.

The boys decided to have fun and came up with a plan. Namely, in some day in the morning Misha will ride the underground from station sto station f by the shortest path, and will draw with aerosol an ugly text "Misha was here" on every station he will pass through (including sand f). After that on the same day at evening Grisha will ride from station t to station f by the shortest path and will count stations with Misha's text. After that at night the underground workers will wash the texts out, because the underground should be clean.

The boys have already chosen three stations a, b and c for each of several following days, one of them should be station s on that day, another should be station f, and the remaining should be station t. They became interested how they should choose these stations s, f, t so that the number Grisha will count is as large as possible. They asked you for help.

Input

The first line contains two integers n and q (2 ≤ n ≤ 105, 1 ≤ q ≤ 105) — the number of stations and the number of days.

The second line contains n - 1 integers p2, p3, ..., p n (1 ≤ p i ≤ n). The integer p i means that there is a route between stations p i and i. It is guaranteed that it's possible to reach every station from any other.

The next q lines contains three integers a, b and c each (1 ≤ a, b, c ≤ n) — the ids of stations chosen by boys for some day. Note that some of these ids could be same.

Output

Print q lines. In the i-th of these lines print the maximum possible number Grisha can get counting when the stations s, t and f are chosen optimally from the three stations on the i-th day.

Examples

1
2
3
4
5
6
7
8
9
10
11
12
13
14
input
3 2
1 1
1 2 3
2 3 3
output
2
3
input
4 1
1 2 3
1 2 3
output
2

Note

In the first example on the first day if s = 1, f = 2, t = 3, Misha would go on the route 1 img 2, and Grisha would go on the route 3 img 1 img 2. He would see the text at the stations 1 and 2. On the second day, if s = 3, f = 2, t = 3, both boys would go on the route 3 img 1 img 2. Grisha would see the text at 3 stations.

In the second examle if s = 1, f = 3, t = 2, Misha would go on the route 1 img 2 img 3, and Grisha would go on the route 2 img 3 and would see the text at both stations.

Key

给一棵树，从中取三点\(a\)、\(b\)、\(c\)，任取其中两点作为起点\(s\)、\(t\)，剩余一点作为终点\(f\)。问“s到f的最短路径”与“t到f的最短路径”重叠部分最大有多少。

使用了LCA与倍增。可以看到，三个点两两搭配的最近公共祖先中，必至少有两对是同一个祖先。

三个点只有以下两种情况：（令\(dep[lca(b,c)]>=dep[lca(a,b)]\)，这样就可以把b、c看作一个整体了（b、c是不是处于一条链、是不是重叠也不影响bc整体与a的判断），此时\(dep[lca(a,b)]\)必等于\(dep[lca(a,c)]\)。） 第一种情况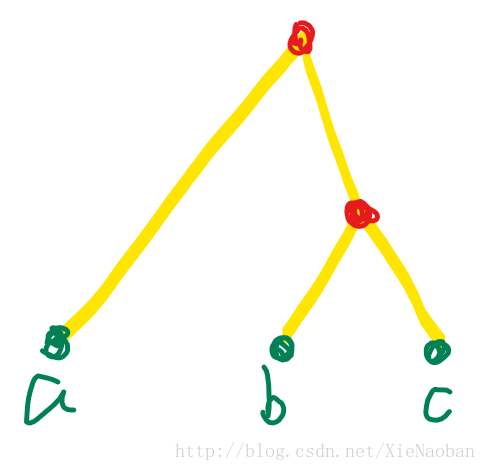： 这里写图片描述 a与bc不在一条链上。·可以看到答案要么是a到\(lca(b,c)\)的距离，要么是b、c分别到\(lca(b,c)\)的距离。

第二种情况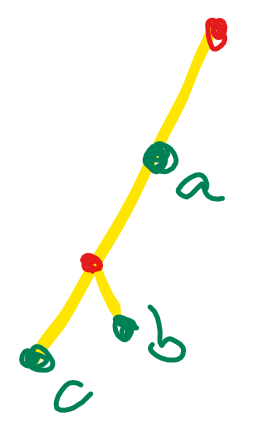： 这里写图片描述 a与bc处于一条链。答案与上面类似，也是三种情况，但是没有经过分叉，计算上略微不同。

然而输入的abc位置随机，直接判断很麻烦。可以像上图一样，把lca深度大的设为b、c，就很方便了。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#define mset(a,b) memset(a,b,sizeof(a))
using namespace std;
const int maxn = (int)1e5 + 10;
int n, q;
int a, b, c;
vector<int> T[maxn];
int d[maxn];
int p[maxn][28];

void dfs(int u) {
	for (auto &i:T[u]) {
		if (i == p[u][0]) continue;
		d[i] = d[u] + 1;
		p[i][0] = u;
		dfs(i);
	}
}

void init() {
	for (int j = 1; (1 << j) <= n; j++) {
		for (int i = 1; i <= n; i++) {
			p[i][j] = p[p[i][j - 1]][j - 1];
		}
	}
}

int lca(int a, int b) {
	if (d[a]>d[b])swap(a, b);
	int f = d[b] - d[a];
	for (int i = 0; (1 << i) <= f; i++) {
		if ((1 << i)&f)b = p[b][i];
	}
	if (a != b) {
		for (int i = (int)log2(n); i >= 0; i--) {
			if (p[a][i] != p[b][i]) {
				a = p[a][i]; b = p[b][i];
			}
		}
		a = p[a][0];
	}
	return a;
}


int main()
{
	mset(d, 0); mset(p, 0);
	ios::sync_with_stdio(false);
	cin >> n >> q;
	for (int i = 2; i <= n; ++i) {
		int p;
		cin >> p;
		T[i].push_back(p);
		T[p].push_back(i);
	}
	dfs(1);
	init();
	while (q--) {
		cin >> a >> b >> c;
		int f1 = lca(a, b);
		int f2 = lca(a, c);
		int f3 = lca(b, c);

		if (d[f1] > d[f2]) {
			swap(b, c);
			swap(f1, f2);
		}
		if (d[f2] > d[f3]) {
			swap(a, b);
			swap(f2, f3);
		}

		int res1 = (f1 == a ? (d[f3] - d[f1]) : (d[a] - d[f1]) + (d[f3] - d[f1]));
		int res2 = max(d[b] - d[f3], d[c] - d[f3]);
		cout << max(res1, res2) + 1 << '\n';
	}
	return 0;
}