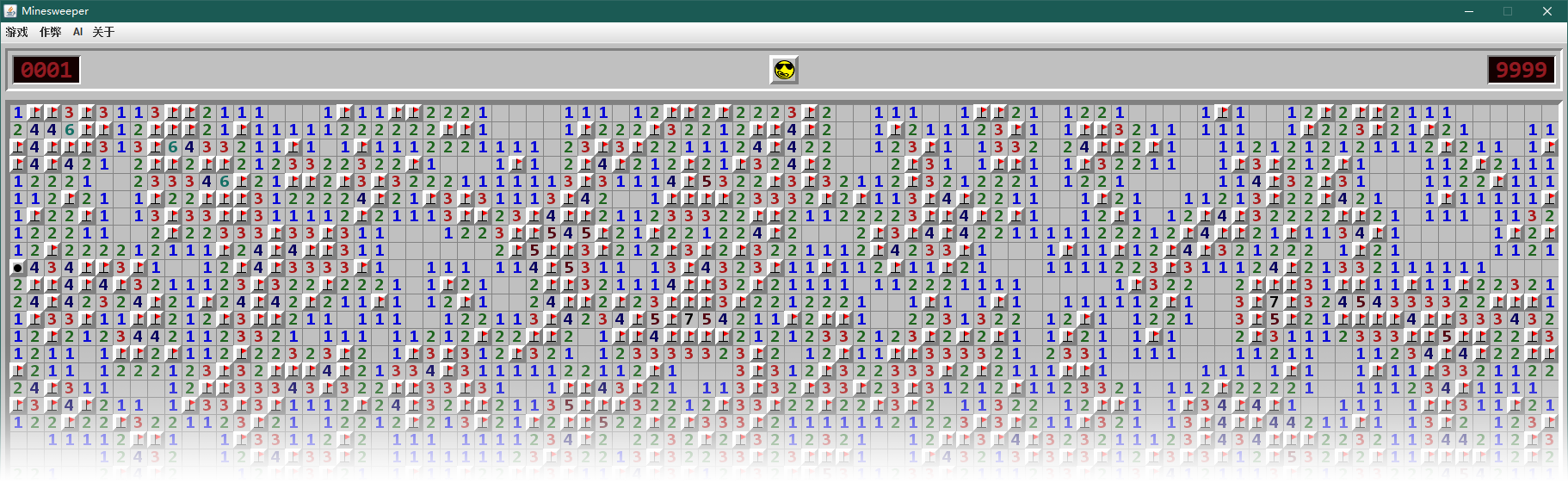
上一篇博客介绍了本项目总体情况, 这一篇来介绍一下我实现的自动扫雷 AI 算法. 本 AI 胜率比网上最高胜率的 AI 差 0.5% 左右. 不过本 AI 也不是没有优势, 它运算速度很快 (强行有优势 (ˉ▽ ̄~)), 平均 42 毫秒可以扫完一局 Win XP 规则下的专家难度.
这篇博客会介绍一下我的思路和踩过的坑, 也会列出一些关于胜率的数据. 希望能够帮助其他萌新入个门. 项目已经开源, 代码也写了注释, 链接放在文章最后.
先再次把最终成品的 AI 胜率等指标罗列一下:
| 指标 | Win XP 规则测试结果 | Win 7 规则测试结果 |
|---|---|---|
| 测试版本 | Win XP 规则, 专家难度 | Win 7 规则, 专家难度 |
| 测试局数 | 50,0000 局 | 50,0000 局 |
| 胜率 | 39.68% | 52.45% |
| 运行总耗时 | 21275 秒 | 33136 秒 |
| 每局平均耗时 | 42 毫秒 | 66 毫秒 |
| 胜局的每局平均耗时 | 57 毫秒 | 68 毫秒 |
注1: 测试 Win XP 规则是在半夜运行的, 电脑除了扫雷没有在运行其他进程; 而测试 Win 7 规则时我同时还在拿电脑办公, 导致 Win 7 规则下耗时比 XP 多. 而实际上 Win XP 与 Win 7 应该运行时间差不多. 注2: 测试使用的扫雷程序是自己复现的 Win XP 与 Win 7 规则, 而非模拟鼠标点击原版扫雷窗口. 因为那样太慢了. 网上有大佬已经测试过, Win XP, Win 7 原版扫雷并无影响地雷分布的隐藏规则. 所以若真要在原版上测试, 结果应该不会有较大偏差.
我在网上找到的胜率最高的扫雷 AI 是 ztxz16 大佬写的, Win XP 版本胜率 40.07%, Win 7 版本胜率 52.98%. 我的做法也是参考了 ztxz16 大佬的算法 (最强扫雷 AI 算法详解 + 源码分享 - ztxz16). B 站的 _黄歪歪 应该也是他, 也发了些关于扫雷 AI 的视频. 膜一波.
不过 ztxz16 大佬的这个项目偏试验性, 我顶着没有注释的压力把大佬开源的源码看了一遍, 看得出来有些地方他应该是懒得优化, 最终 AI 速度不是很快. 我本来想自己测试一遍他的 AI, 但跑了一晚上也只跑出来了几千局还是几万局 (捂脸).
该交代的差不多都交代完了, 下面开始讲我的做法.
高胜率低耗时自动扫雷 AI 算法
术语与定义
统一一下一些操作的术语方便后续描述. 我不是扫雷圈的, 很多术语可能不知道, 所以如果以下操作本来就有自己的中文名称, 提醒我我会改过来的!
| 操作 | 术语 |
|---|---|
| 鼠标左键, 那个点开格子的操作 | 挖掘 |
| 鼠标右键, 那个放置小红旗的操作 | 插旗 |
| 鼠标双键或中键, 那个自动检测周围八格是否可挖掘的操作 | 检查周围 |
| 空白的, 没点过的格子 | 未知格 |
| 已知的有数字 (包括 0) 的格子 (已挖开且不是雷的格子) | 数字格 |
另外, 1. 格子坐标 \((x, y)\) 表示 \(x\) 行 \(y\) 列, 下标从 \(0\) 开始. 2. \(N\) 和 \(M\) 为棋盘行数与列数, \(S = N \times M\) 表示格子总数. 3. 以下所涉及的 "胜率", 除非另外注明, 均为 Win XP 规则专家难度下的胜率.
第一步: 开局挖哪
开局第一步点击不同的地方也是会影响胜率的. 根据 ztxz16 大佬的测试 (地表最强扫雷AI • 编程探索扫雷极限胜率 - _黄歪歪), 开局 Win XP 挖掘 \((0, 0)\), Win 7 挖掘 \((2, 2)\) (或对称的另外三个角落) 胜率最高.
我自己也对 Win XP 与 Win7 大致测了一下 \((0, 1)\), \((1, 0)\), \((1, 1)\) 等几个位置, 确实如此, 胜率会下降 1% ~ 2% 左右.
 |
 |
|---|---|
| Win XP 开局 \((0, 0)\) | Win 7 开局 \((2, 2)\) |
不过至于为什么是角落胜率比中心高, 我猜可能是角落有更多可套用减法公式的场景 (减法公式在下一节有讲). 减法公式本质就是根据相邻两个数字格的一侧去推断另一侧. 而边缘的格子天然已知靠边的一侧无雷, 因而可以更容易地推断出另一侧雷的个数.
第二步: 基于定义与定式
用到了两个基本公式或定式:
第一, 仅基于一格判断: 即根据目标数字格的数字与其周围八格 (角落的话不满八格) 的状态, 判断该数字格周围八格的未知格是不是全为雷或全不为雷. 这是扫雷最基本的公式. 其逻辑其实就是鼠标左右双键检查周围的逻辑.
第二, 基于相邻两格: 即使用减法公式.

如图, \(M\), \(N\) 为两个相邻数字格, 两者上下各有一块互相影响的公共区域 \(P\), \(Q\), 左右则分别有互不影响的两翼 \(A\), \(B\). 记地雷数量为 \(C\), 显然地雷数量 \(C\) 符合如下等式:
\[ \begin{cases} C_{AroundM} = C_A + C_P + C_Q \\ C_{AroundN} = C_B + C_P + C_Q \end{cases} \]
两式相减即得减法公式:
\[ C_{AroundM} - C_{AroundN} = C_A - C_B \]
即 \(M\) 与 \(N\) 的数字之差就是 \(A\) 与 \(B\) 雷数量之差.
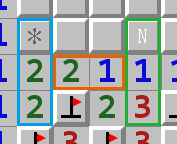
举个简单的例子: 如下方案例图 1 两个数字格 \(2 - 1 = 1\), 即蓝色区域比绿色区域多一个雷, 而蓝色区域三个格子有两个已知不是雷, 故而可推得蓝色区域有且只有一个雷, 这个雷只能在 * 处. 既然蓝区有一个雷, 绿区就有 \(1 - 1 = 0\) 个雷, 故而 N 处必为一个数字格.
 |
 |
|---|---|
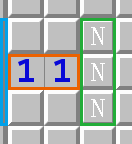
| 案例图 1 | 案例图 2 |
而如果相邻两格的一侧在棋盘边缘, 如案例图 2 所示, 蓝区在棋盘外, 即蓝区无雷, 而 \(M - N = 0\), 故绿区均不为雷.
可见减法公式在边缘有更多的使用场景, 这可能也是开局要挖角落的原因之一.
关于减法公式更详细的内容可以参考这篇专栏: 扫雷新手判雷上路(一)——初步认识减法公式及其衍生的最简单定式 - MsPVZ.ZSW.
截至这一步的胜率与耗时
如果仅仅使用基本定式, 遇到定式无法解决的就投降判负, 胜率在 5% 左右 (毕竟如果开局就点了个 '1', 那就直接无了).
而如果仅使用基本定式, 遇到定式无法解决的就瞎猜, 胜率就已经有 23% 了.
平均每局耗时在 4ms 以下, 没精确测过. 基于定式的算法虽然使用场景较为受限, 但效率非常高, 扫完一整局的时间复杂度也就 \(O(S)\).
第三步: 基于每个格子可能有雷的概率
针对某一棋局局面, 每个未知格有雷的概率当然是可以计算出来的, 即
\[ 目标未知格含雷概率 = \frac{目标未知格含雷的方案数量}{局面所有可行方案数量} \]
扫的时候谁有雷的概率最低就扫谁.
局面所有可行方案的计算方法用回溯法即可. 当然直接就对所有未知格进行回溯的话复杂度有 \(O(2^S)\) 自然受不了, 所以这一步的算法主要难点是剪枝.
如何剪枝, 可以用下面这张图很直观地展现出来:
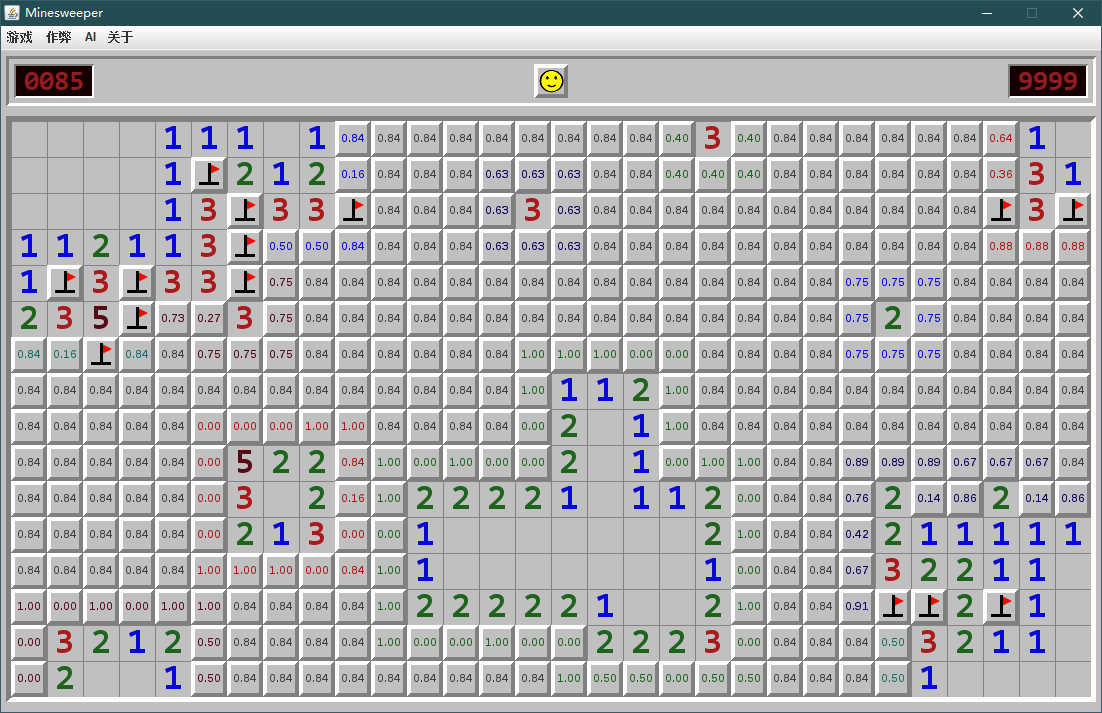
在上图中, 每个未知格上都被打上了该格子的非雷概率 (注意, 这张图上展示的是 "非雷概率", 也就是 \(1 - P_{有雷}\)), 且与数字格相邻的未知格均被用彩色高亮了出来; 而不与数字格相邻的未知格则均用灰色标识.
不知道怎么取名, 这里我姑且将所有相近的 (不一定紧挨)、相同颜色的未知格集合称作一个 "连通分量", 而剩下所有灰色格子姑且称之为 "孤立格". 而本小节最重要的两个步骤就是①计算出所有连通分量, ②基于连通分量计算出每个未知格的有雷概率.
计算连通分量
回溯法剪枝其实就是要分隔出尽可能短的连通分量, 然后在每个连通分量上回溯出所有可能方案, 最后合并所有连通分量的方案.
首先不太严谨地定义一下 "连通分量". 在不考虑剩余雷数制约的前提下, 如果一个未知格 A 最终挖开的不同状态 (数字或雷) 会影响另一个未知格 B 不同状态的概率分布 (反过来 B 的状态也会影响 A), 则认为 A、B 同属一个连通分量. 且若 A、B 同属一个连通分量, B、C 同属一个连通分量, 则 A、B、C 同属一个连通分量.
放到实际计算中, 其实就很简单:
- 从任意数字格开始, 找出其周围八格中所有未知格, 并加入队列;
- 取队列中一未知格, 找出其周围八格中所有数字格, 再分别找出这些数字格周围八格的未知格入队列 (不重复入队).
- 重复 2 直到队列为空. 在队列里存在过的所有未知格均属同一连通分量.
用上述方法计算得的连通分量内部其实依然可能存在互不影响的部分, 可以进一步优化, 将一个连通分量拆成多个更短的连通分量.
优化方法也很简单, 如果已经能确定某个未知格是雷, 请把他插上小红旗 (网上看了很多 AI 不喜欢插旗). 如下两张图所示.
 |
 |
|---|---|
| 不插旗时找出的连通分量 (深红) | 插了旗后找出的连通分量 (青色、深红) |
计算有雷概率
(公式敲的我头昏脑胀, 如有错误请指正)
回溯枚举所有 \(K\) 个连通分量, 可以得到如下结果:
对于 \(\forall c \ge 0\), \(\forall i \in [1, K]\), \(\forall j \in [1, Len(CC_i)]\),
- \(TotalCnt_{(i, c)}\) - 当连通分量 \(CC_i\) 中一共有 \(c\) 个雷时的所有可行方案个数.
- \(MineCnt_{(i, j, c)}\) - 当连通分量 \(CC_i\) 中一共有 \(c\) 个雷时, 属于 \(CC_i\) 的格子 \(Cell_{(i, j)}\) 在所有 \(TotalCnt_{(i, c)}\) 个可行方案中有雷的次数.
由上述信息可以计算, 前 \(k\) 个连通分量 \(CC_1 \sim CC_k\) 作为一个整体一共有 \(c\) 个雷时的方案数:
\[ \begin{aligned} MultiCnt_{(1 \sim k, c)} & = \sum_{s = 0}^c MultiCnt_{(1 \sim k - 1, s)} \times TotalCnt_{(k, c - s)} & (1) \\ & = \sum_{s = 0}^c MultiCnt_{(1 \sim i - 1, s)} \times MultiCnt_{(i \sim k, c - s)}, i \in [2, k] & (2) \end{aligned} \]
在实际编程中, 会涉及大量计算 \(MultiCnt_{(\text{except }i, c)}\). 使用上面 \((1)\) 动态规划, 使用 \((2)\) 从左右双向记忆化, 能节约点计算.
然后对于所有不属于任何连通分量的孤立格, 我们也要计算它们的可行方案数. 若 \(b\) 个孤立格中有 \(c\) 个雷, 则这些孤立格的可行方案数为:
\[ IsolCnt_{(b, c)} = IsolCnt_{(b - 1, c)} + IsolCnt_{(b - 1, c - 1)} \]
实际实现中我直接打了个 \(16 \times 30 \times 99\) 的表.
于是可以计算, 所有 \(b\) 个孤立格与指定连通分量集合 \(T\) 在有 \(c\) 个雷的情况下的可行方案数为:
\[ Cnt_{(T, c)} = \sum_{s = 0}^c MultiCnt_{(T, s)} \times IsolCnt_{(b, c - s)} \]
于是, 对于任意连通分量的任意格子 \(Cell_{(i, j)}\), 一共 \(c\) 个雷, \(K\) 个连通分量, 其有雷概率为:
\[ MineProb_{(i, j)} = \frac{\sum_{s = 0}^c Cnt_{(\text{except }i, s)} \times MineCnt_{(i, j, c - s)}}{Cnt_{(1 \sim K, c)}} \]
有了每个连通分量的格子的概率, 孤立格子的概率就很好算了:
\[ MineProb_{\text{isol}} = \frac{c - \sum_{i}\sum_{j}MineProb_{(i, j)}}{b} \]
由此我们就计算出了所有未知格的有雷概率.
附加小策略小技巧
当有雷概率最低的未知格有不止一个时, 也有些小策略可以增加胜率. 经过实际测试, 目前我采用了以下策略, 能提升 2% 左右:
- 优先选择在四个角落的格子;
- 当两者都在 (或都不在) 角落时, 选择周围 24 格中数字格最多的.
截至这一步的胜率与耗时
这一步的算法的使用场景是覆盖了基本定式那一步的, 即定式能做的概率也能做. 但定式速度快, 所以仍有存在意义. 测了十来万盘, "定式 + 概率" 策略的胜率在 36% ~ 37% 左右, 平均每局耗时 6ms.
(一开始我没有将连通分量的不同雷数分开考虑, 而是根据连通分量的平均雷数来计算, 导致胜率只有 32%, 可见近似算法差距还是很大的.)
而加上了那些小策略后, 胜率提升到了 38.5%.
极端情况:
到这里你可能有疑问, 剪枝确实很高效, 但如果遇到极端情况不是依然得爆炸?
答案是肯定的. 但是经过我这么多次的测试, 基本上 1,0000 局里也很难遇上极端情况.
但如果您真的很迫切地想看我的 AI 出丑也没关系, 我亲自在项目根目录放了一个难以剪枝的残局案例, 保证让您风扇起飞.

第四步: 基于对下一局面的有限预测
这一步是我瞎想的, 没想到真的有用. 想到这一步的主要原因是, 无雷概率高不完全等于获胜概率高; 而计算胜率又绝大部分情况下不可行. 于是就想着整个折中方案.
这一步是针对上一步有雷概率计算出现多个格子有最低有雷概率的情况. 本策略会覆盖上面说的小策略小技巧, 但又由于本策略复杂度不低, 所以当判断发现计算量过大时还是采用之前的小策略小技巧.
原理是, 对于每个有雷概率最低的格子, 计算: 选择该格子后, 可被百分百确定的其他未知格的期望数量. 方法是, 枚举格子的所有可能性 (0 ~ 8, 雷), 使用上一步的概率计算这一假设的新局面中所有格子的非雷概率. 最后统计每个新局面必然非雷的格子个数, 计算一下它们的平均值.
最后我们选择期望值最高的格子.
截至这一步的胜率与耗时
测了万把盘, 胜率达到 39.3%, 平均每局耗 8ms 多.
这一步我做的比较保守, 因为我不知道有没有可能出现 "非雷概率 A > B" 但 "胜率 A < B" 的情况.
第五步: 基于胜率 (最终杀招)
最后一招, 直接把每个未知格的胜率算出来.
这里区分一下 "获胜概率" 与第三步的 "有雷概率". 胜率是指挖掘某个未知格的最终获胜概率; 有雷概率是指当前局面下未知格是雷的概率. 显然, 当前局面所有未知格中最高的胜率代表了这个残局的整体胜率.
这世上没有什么策略比直接算胜率更准了, 但可惜它的复杂度过于恐怖, 所以我只在当残余未知格少于等于 12 时才会启用这个策略.
算法原理还是动态规划. 设 \(b\) 为当前局面, \(b_{(x, y)}\) 为将未知格 \(x\) 设为数字 \(y\) 的下一局面. 另设 \(CellWinRate()\) 为某格子的胜率, \(BoardWinRate()\) 为某局面的胜率, \(Cnt()\) 为某局面的所有可行方案个数.
\[ \begin{aligned} BoardWinRate(b) & = \underset{x}{\text{Max}}(CellWinRate(b, x)) \\ CellWinRate(b, x) & = \sum_{y=0}^{8}BoardWinRate(b_{(x, y)}) \times \frac{Cnt(b_{(x, y)})}{Cnt(b)} \end{aligned} \]
每个局面 \(b\) 可以状态压缩, 用一个 String 表示, 方便记忆化搜索.
胜率算法计算完后就很简单了, 胜率最高的格子随便挑一个挖. 而且所有后续局面的胜率也在之前的计算中缓存过了, 从缓存里掏出来一路扫到结束即可.
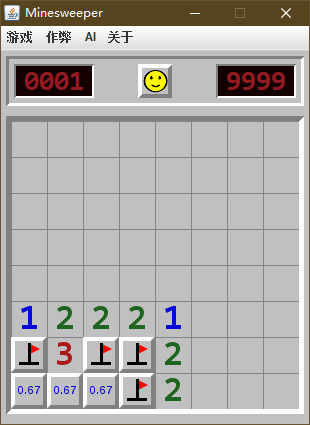
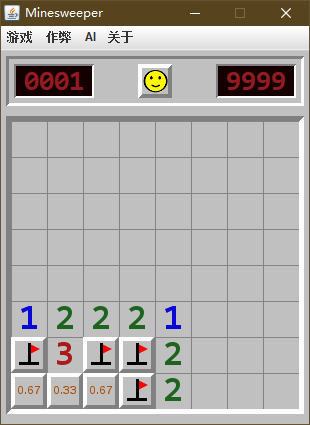
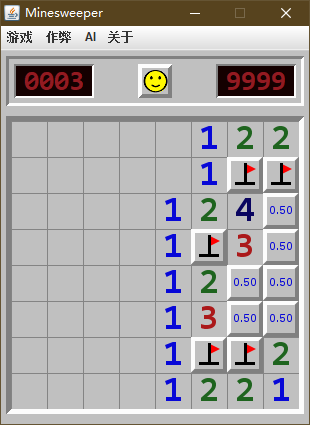
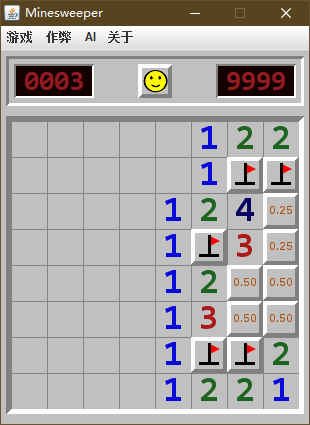
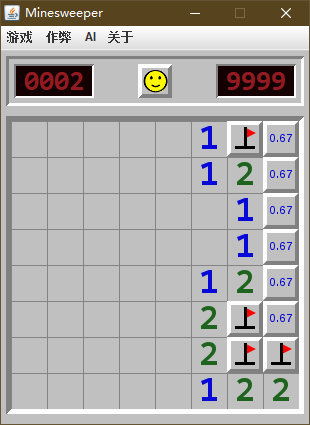
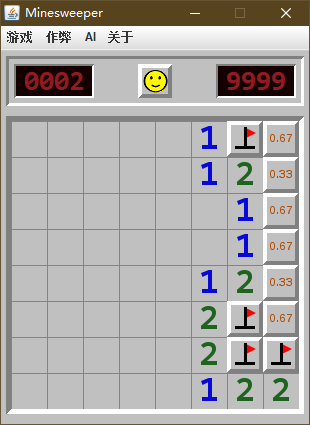
我自己整理了几个 "无雷概率" 与 "获胜概率" 区别的例子 (这里是无雷概率, 为了方便与胜率对比), 可以帮助理解一下:
| 无雷概率 | 获胜概率 |
|---|---|
 |
 |
 |
 |
 |
 |
更多对比案例可以在我的 Github 项目根目录找到.
衍生
最后我稍微衍生了一下使用场景. 如果某个区域只可能有 \(c\) 个雷 (雷数可确定, 比如幸福三选一), 那这片区域也能套用胜率算法直接扫掉, 姑且叫之局部胜率. 这个操作不会影响总体胜率, 但能稍微提一丢丢速 (指爆雷重开的速度... 早发现早治疗, 早暴毙早投胎).
最终胜率与概率
已经写在博文最上面了. 50 万局测试, 胜率 39.68%, 平均每局 42ms.
附: 探索百分比
测试 50 万盘的时候顺便记录了一下每一局不论输赢都探索到了什么程度 (游戏结束前被扫开的格子占所有格子的百分比). 虽然不知道有什么用但也列一下 (柱状图是我在命令行里画的, 有点写意):
1 | Win XP 规则专家难度 50,0000 局: |
1 | Win 7 规则专家难度 50,0000 局: |
这么看确实 Win XP 下开局劝退得有点离谱.
源码
本博客仅发布于 Github IO: https://xienaoban.github.io/posts/62679.html
和 CSDN: https://blog.csdn.net/xienaoban/article/details/112424633
其他都是盗的.
项目源码 Github: https://github.com/xienaoban/minesweeper (喜欢的话 Star 一下呀 (づ ̄3 ̄)づ╭❤~)
不会用 Github 的萌新也可以在这里下载: https://download.csdn.net/download/XieNaoban/14090898
主要有以下几个文件:
1 | AutoSweeper.java // 自动扫雷 AI |
其中 AutoSweeper.java 和 MineSweeper.java 写的比较上心, 有较为详细的注释, 代码结构也相对清晰. 别的几个文件就写的比较写意, 酌情观看.