逻辑回归算法是分类算法，虽然这个算法的名字中出现了“回归”，但逻辑回归算法实际上是一种分类算法，我们将它作为分类算法使用。。 分类问题：对于每个样本，判断它属于N个类中的那个类或哪几个类。通常我们判定一个样本，若我们预测它的确属于这个类的可能性大于50%，则认为它属于这个类。当然具体选择50%还是70%还是其他要看具体情况，这里先默认50%。 线性回归的局限性在分类问题的例子中变得不可靠：这是一个用来预测肿瘤是否呈阴性的模型，当一个肿瘤的尺寸大于一个数，我们就认为这个肿瘤呈阴性。我们现在新增了一个数据，结果导致整个模型的参数变化很大。如下图，在新加入最右侧数据后，50%的分水岭右移了不止一点点。而根据常识这个数据本应对我们的预测没有什么影响。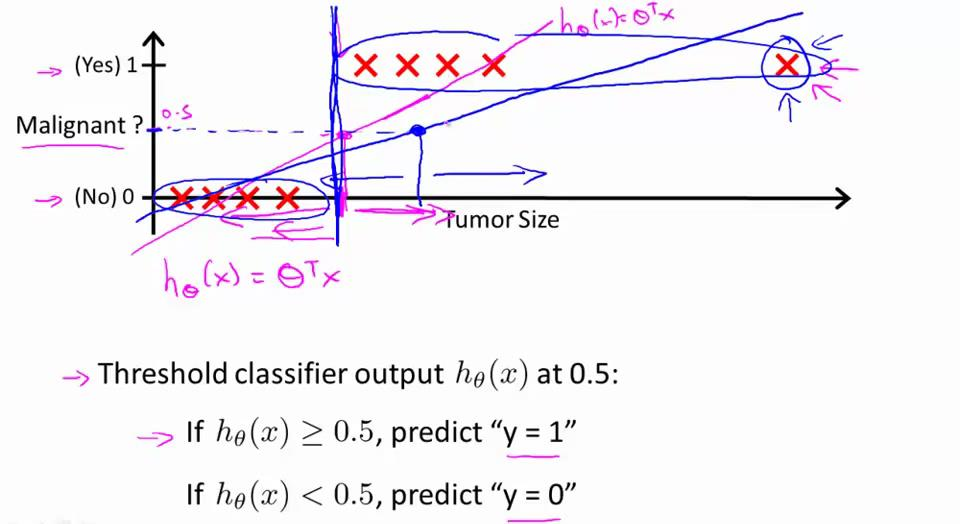 
对此类问题引入新模型：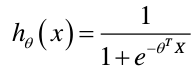 
对于g(z)=1/(1+e^(-z))这个模型，对国内读过高中的学生都能看懂都想得出它的函数图像，当z>0时g大于0.5，z<0时g小于0.5，z=0时g=0.5。我们以此判定样本属于一个类的几率。现在上图这个模型就是g(theta.T X)（“.T”代表转置矩阵），即我们需要找到参数区分出50%这一边界。 对于下图的数据，我们只需使用一条直线分出0.5的交界处即可。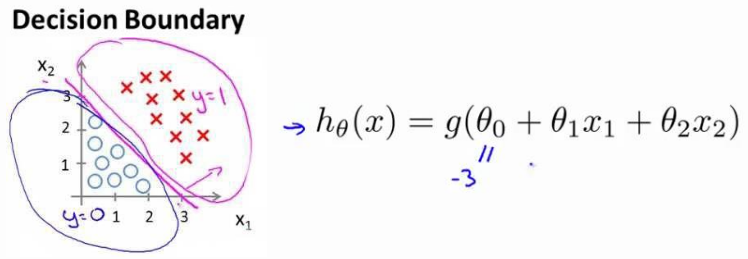 
而对于下面的数据，我们觉得得使用曲线来适应才能分割y=0与y=1的区域。h(x)如图所示，最终得到一个类似圆形的形状。 
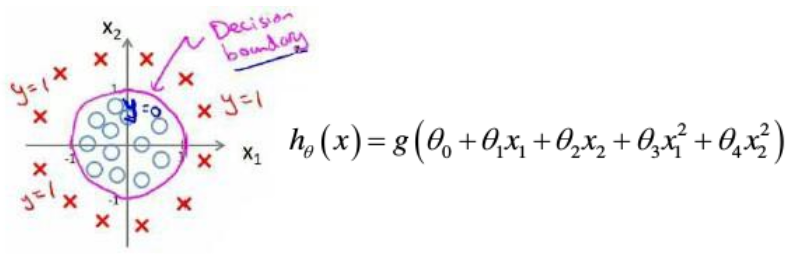对于更复杂的形状，我们可以使用更为复杂的模型。 不过以上的分类问题只有两个类（叫做二元分类问题），只需回答一个数据属于A还是B即可。后面还有复杂些的多类别分类，后面会讲，先仅仅分析叫做二元分类。
1.二元分类问题的代价函数
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们 也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将h(x) 带入到线性回归模型适用的代价函数中时,我们得到的代价函数将是一个非凸函数(non-convex function)。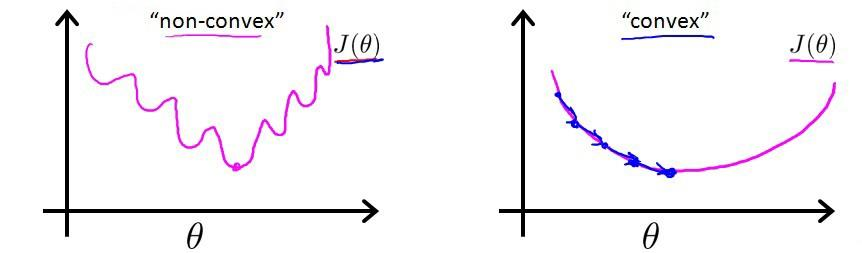 
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值（是的即将讲的新模型能够确保找到全局最小值，因为它是凸函数(convex)，只有一个极小值，那就是最小值。具体下面讲）。 于是重新定义逻辑回归的代价函数：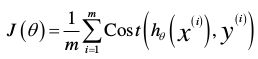 
其中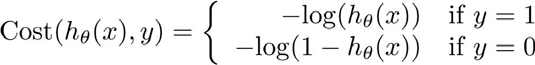 
简化上式得：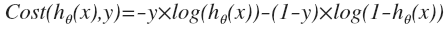 
Cost带入J最终得到的代价函数：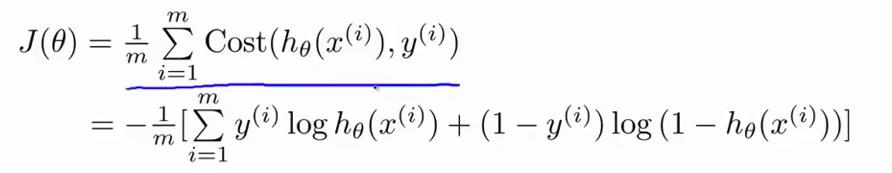 
h(x)与 Cost(h(x),y)之间的关系如下图所示：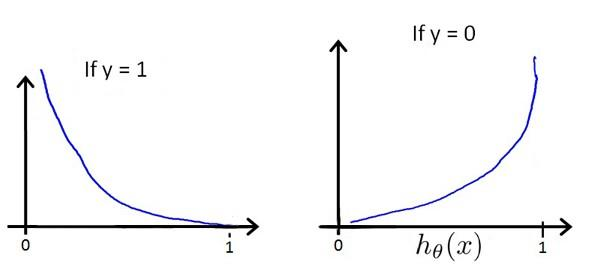 
这样构建的Cost(h θ (x),y)函数的特点是:当实际的y=1且 h也为1时误差为0，当y=1但h不为1时误差随着h的变小而变大；当实际的y=0且h也为0时代价为0，当y=0但h不为0时误差随着h的变大而变大。
2.对二元分类问题使用梯度下降
知道了代价函数然后像对线性回归一样使用梯度下降算法：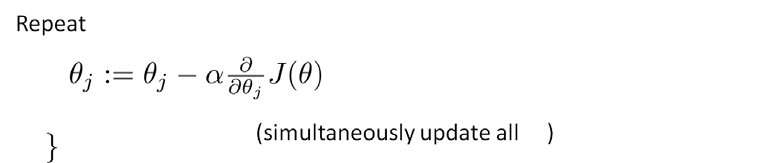 
求导后得到： 
（原视频少了1/m！我用红色补上了。）
于是乎我们惊奇的发现，这个式子的样子和之前用在线性回归的一样！而他们的J(θ)显然是不一样的。那么,线性回归和逻辑回归是同一个算法吗？ 显然不是，要知道，我们是对x求导，而不是对h(x)求导，而两者的h(x)完全不同，所以求导的过程中要展开h(x)对x进行求导，所以结果其实是完全不同的。只不过这两个求导结果刚好可以重新用h(x)包装起来表示。所以逻辑函数的梯度下降，跟线性回归的梯度下降实际上是两个完全不同的东西。
特征缩放
与线性回归一样的是，别忘记特征缩放。这很重要，特征缩放后可以更快地到达最优解，并防止反复的震荡。具体不再展开讲了。
梯度下降必能找到该代价函数的全局最小值
In this video, we will define the cost function for a single train example. The topic of convexity analysis is now beyond the scope of this course, but it is possible to show that with a particular choice of cost function, this will give a convex optimization problem. Overall cost function j of theta will be convex and local optima free. 在这个视频中，我们定义了单训练样本的代价函数,凸性分析的内容是超出这门课的范围的，但是可以证明我们所选的代价值函数会给我们一个凸优化问题。代价函数 J(θ)会是一个凸函数，并且没有局部最优值。
吴恩达老师的视频这里说了这个新的代价函数是凸函数，所以使用梯度下降一定能达到全局最小值。证明我也暂时不管它了。
3.多类别分类（Multiclass Classification）
上面讲了二元分类问题的计算方法，但是如果问题有很多个类，要你预测样本属于这么多类里的哪一个，要怎么做呢？通常我们使用“一对余”方法。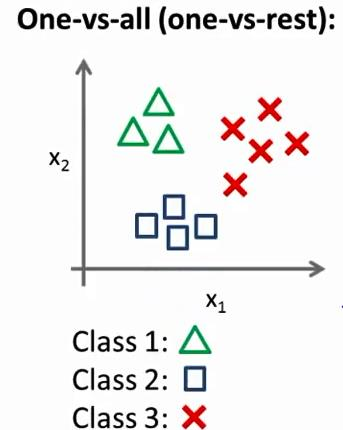 
“一对余”方法：将“n类别问题”转换成“n个二元分类问题”。 比如现在有3个类ABC要划分，我们对每个类单独进行分析。比如对于类B，把所有数据划分成两类，属于B的（正样本）和不属于B的（负样本），我们不需要知道它是属于A还是C的，只需知道它不是B即可。于是对于每个类都变成了一个二元问题，一共3个二元问题。我们要做的就是训练这三个分类器。当预测一个新数据的分类时，我们选择3个h(x)里值最高的那个。 
4.最小化代价函数的其他算法
一些梯度下降算法之外的选择：除了梯度下降算法以外，还有一些常被用来令代价函数最小的算法，这些算法更加复杂和优越，而且通常不需要人工选择学习率，通常比梯度下降算法要更加快速。这些算法有：共轭梯度(Conjugate Gradient)，局部优化法(Broyden fletchergoldfarb shann,BFGS，或叫变尺度法)和有限内存局部优化法(L-BFGS，或叫限制变尺度法)。虽然我暂时不打算看，但Mark一下。