千年两小时只写出2题，这次终于把C题写出来了。。。

Description

On the way to school, Karen became fixated on the puzzle game on her phone!

The game is played as follows. In each level, you have a grid with n rows and m columns. Each cell originally contains the number 0.

One move consists of choosing one row or column, and adding 1 to all of the cells in that row or column.

To win the level, after all the moves, the number in the cell at the i-th row and j-th column should be equal to gi, j.

Karen is stuck on one level, and wants to know a way to beat this level using the minimum number of moves. Please, help her with this task!

Input

The first line of input contains two integers, n and m (1 ≤ n, m ≤ 100), the number of rows and the number of columns in the grid, respectively.

The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains gi, j (0 ≤ gi, j ≤ 500).

Output

If there is an error and it is actually not possible to beat the level, output a single integer -1.

Otherwise, on the first line, output a single integer k, the minimum number of moves necessary to beat the level.

The next k lines should each contain one of the following, describing the moves in the order they must be done:

row x, (1 ≤ x ≤ n) describing a move of the form "choose the x-th row". col x, (1 ≤ x ≤ m) describing a move of the form "choose the x-th column". If there are multiple optimal solutions, output any one of them.

Examples

input
3 5
2 2 2 3 2
0 0 0 1 0
1 1 1 2 1
output
4
row 1
row 1
col 4
row 3
input
3 3
0 0 0
0 1 0
0 0 0
output
-1
input
3 3
1 1 1
1 1 1
1 1 1
output
3
row 1
row 2
row 3

Note

In the first test case, Karen has a grid with 3 rows and 5 columns. She can perform the following 4 moves to beat the level: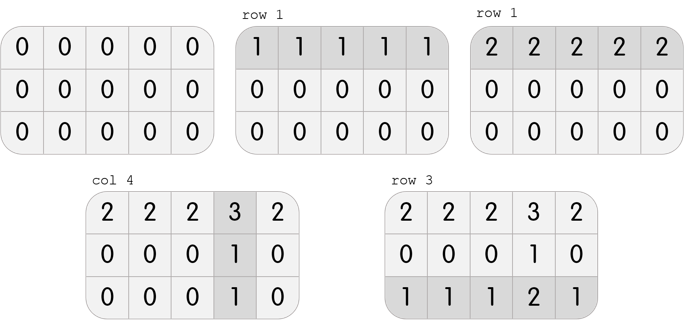

In the second test case, Karen has a grid with 3 rows and 3 columns. It is clear that it is impossible to beat the level; performing any move will create three 1s on the grid, but it is required to only have one 1 in the center.

In the third test case, Karen has a grid with 3 rows and 3 columns. She can perform the following 3 moves to beat the level: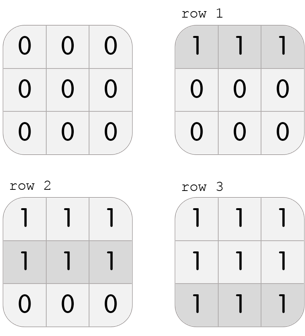

Note that this is not the only solution; another solution, among others, is col 1, col 2, col 3.

Key

有一个有n*m个单元的、每个单元填有数字的网格，每次操作可将某一整行、一整列的单元数值-1，问最少进行多少次操作可以将网格所有单元减到0。

模拟。对每一行/列模拟即可。对于3*5的网格，如果要把每一个单元的数值-1，按行减，要3次，按列减，要5次。所以模拟的时候肯定是优先按行数/列数小的那一个开始减，每次减到该行/列出现0则无法再减，跳转下一行/列。模拟到最后遍历一遍查看有没有个别单元无法减到0，若有则输出-1。

Code

#include<iostream>
#include<cstring>
using namespace std;
int n, m;
int arr[123][123];
int minr[123], minc[123];
int main()
{
	ios::sync_with_stdio(false);
	memset(minr, 1, sizeof(minr));
	memset(minc, 1, sizeof(minc));
	cin >> n >> m;
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < m; ++j) {
			int &now = arr[i][j];
			cin >> now;
			if (minr[i] > now) minr[i] = now;
			if (minc[j] > now) minc[j] = now;
		}
	}
	int res = 0;
	if (n <= m) {
		int rminr = 9999999;
		for (int i = 0; i < n; ++i) {
			res += minr[i];
			if (rminr > minr[i]) rminr = minr[i];
		}
		for (int i = 0; i < m; ++i) {
			res += (minc[i] -= rminr);
		}
	}
	else {
		int cminc = 9999999;
		for (int i = 0; i < m; ++i) {
			res += minc[i];
			if (cminc > minc[i]) cminc = minc[i];
		}
		for (int i = 0; i < n; ++i) {
			res += (minr[i] -= cminc);
		}
	}
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < m; ++j) {
			if (arr[i][j] - minr[i] - minc[j]) {
				cout << "-1\n";
				return 0;
			}
		}
	}
	cout << res << '\n';
	for (int i = 0; i < n; ++i) {
		while (minr[i]--) cout << "row " << (i + 1) << '\n';
	}
	for (int i = 0; i < m; ++i) {
		while (minc[i]--) cout << "col " << (i + 1) << '\n';
	}
	return 0;
}

XieNaoban's Blog

Codeforces 815A - Karen and Game