#Description There are n cities in Berland, each of them has a unique id — an integer from 1 to n, the capital is the one with id 1. Now there is a serious problem in Berland with roads — there are no roads.
That is why there was a decision to build n - 1 roads so that there will be exactly one simple path between each pair of cities.
In the construction plan t integers a1, a2, ..., at were stated, where t equals to the distance from the capital to the most distant city, concerning new roads. ai equals the number of cities which should be at the distance i from the capital. The distance between two cities is the number of roads one has to pass on the way from one city to another.
Also, it was decided that among all the cities except the capital there should be exactly k cities with exactly one road going from each of them. Such cities are dead-ends and can't be economically attractive. In calculation of these cities the capital is not taken into consideration regardless of the number of roads from it.
Your task is to offer a plan of road's construction which satisfies all the described conditions or to inform that it is impossible.
#Input The first line contains three positive numbers n, t and k (2 ≤ n ≤ 2·105, 1 ≤ t, k < n) — the distance to the most distant city from the capital and the number of cities which should be dead-ends (the capital in this number is not taken into consideration).
The second line contains a sequence of t integers a1, a2, ..., at (1 ≤ ai < n), the i-th number is the number of cities which should be at the distance i from the capital. It is guaranteed that the sum of all the values ai equals n - 1.
#Output If it is impossible to built roads which satisfy all conditions, print -1.
Otherwise, in the first line print one integer n — the number of cities in Berland. In the each of the next n - 1 line print two integers — the ids of cities that are connected by a road. Each road should be printed exactly once. You can print the roads and the cities connected by a road in any order.
If there are multiple answers, print any of them. Remember that the capital has id 1.
#Examples 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39input
7 3 3
2 3 1
output
7
1 3
2 1
2 6
2 4
7 4
3 5
input
14 5 6
4 4 2 2 1
output
14
3 1
1 4
11 6
1 2
10 13
6 10
10 12
14 12
8 4
5 1
3 7
2 6
5 9
input
3 1 1
2
output
-1
#Key 题意：给一棵一共有\(n\)个结点（包括根节点）的树，一共有\(t+1\)层。除第一层只有一个根节点外，给出了其他每层的节点数。已知有\(k\)个结点没有子节点，要求用\(n-1\)个树枝连接所有结点，给出一种可能的连法。 可能的连法（可能）有很多，只要输出随便其中一个即可。
思路：先遍历一遍所有层，求出可行的最大最小的maxk、mink。如果题目给的k不在此范围内，则说明不能组成符合要求的树。这是唯二输出“-1”的情况。
求能产生的最少的无儿子结点：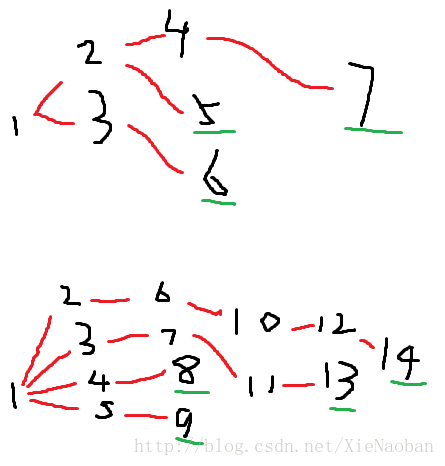 
求能产生的最多的无儿子结点：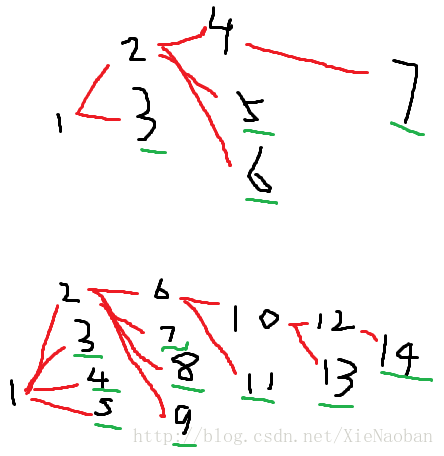 
令\(needk=k-mink\)，则除去一定有的无儿子结点，还有needk个无儿子结点需要手动产生。 然后遍历每一层，自己做出needk个无儿子结点即可。无需建立树，边遍历边输出。
第一次写出了最后一题，开心的一匹(ง •̀▿•́)ง。虽然写了就知道并不难。。。
#Code 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86#include<cstdio>
int n, t, k;
int arr[200010];
int main()
{
scanf("%d%d%d", &n, &t, &k);
arr[0] = 1;
for (int i = 1;i <= t;++i) {
scanf("%d", arr + i);
}
arr[t + 1] = 0;
int mink = 0;
int maxk = 0;
for (int i = 0;i <= t;++i) {
maxk += arr[i] - 1;
if (arr[i] > arr[i + 1])
mink += arr[i] - arr[i + 1];
}
++maxk;
if (mink > k || maxk < k) {
printf("-1");
return 0;
}
printf("%d\n", n);
int needk = k - mink; // dead-ends that needed to created by myself
int nown = 1;
for (int i = 0;i != t;++i) {
int nextn = nown + arr[i];
if (!needk) {
if (arr[i + 1] >= arr[i]) {
int err = arr[i + 1] - arr[i] + 1;
int rem = arr[i] - 1;
for (int j = 0;j != err;++j) {
printf("%d %d\n", nown, nextn++);
}
++nown;
for (int j = 0;j != rem;++j) {
printf("%d %d\n", nown++, nextn++);
}
}
else { // arr[i + 1] < arr[i]
for (int j = 0;j != arr[i + 1];++j) {
printf("%d %d\n", nown++, nextn++);
}
nown += arr[i] - arr[i + 1];
}
}
else {
if (arr[i + 1] >= arr[i]) {
int nextnown = nextn;
int nextnextn = nextn + arr[i + 1];
int err = arr[i + 1] - arr[i] + 1;
for (int j = 0;j != err;++j) {
printf("%d %d\n", nown, nextn++);
}
while (nextn != nextnextn) {
if (!needk) break;
--needk;
printf("%d %d\n", nown, nextn++);
}
++nown;
while (nextn != nextnextn) {
printf("%d %d\n", nown++, nextn++);
}
nown = nextnown;
}
else { // arr[i + 1] < arr[i]
int nextnown = nextn;
int nextnextn = nextn + arr[i + 1];
printf("%d %d\n", nown, nextn++);
while (nextn != nextnextn) {
if (!needk) break;
--needk;
printf("%d %d\n", nown, nextn++);
}
++nown;
while (nextn != nextnextn) {
printf("%d %d\n", nown++, nextn++);
}
nown = nextnown;
}
}
}
return 0;
}