[TOC]
激活函数
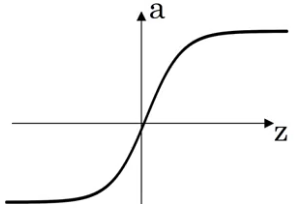
Sigmoid 不怎么用了. \(a = g(z) = \sigma(z) = \frac{1}{1+e^{-z}} \\ g'(z) = a(1-a)\)
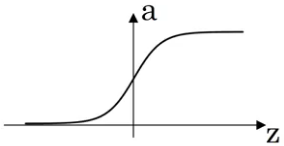
Tanh 比Sigmoid好. 因为其值域为(-1, 1), 计算得a的平均值靠近0, 更好的centers the data(不知道怎么翻译比较好), 有利于下一层的计算. \(a = g(z) = tanh(z) = \frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} \\ g'(z) = 1 - (tanh(z))^2\)
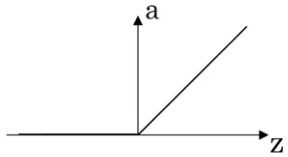
ReLU(Rectified Linear Unit) 收敛快. \(a = g(z) = max(0, z) \\ g'(z) = \begin{cases} 0 &\text{if } z<0 \\ 1 &\text{if } z>0 \\ undefined &\text{if } z=0 \end{cases}\)
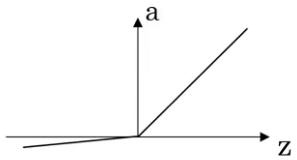
Leaky ReLU 比ReLU更优, 但不怎么用? \(a = g(z) = max(0.01z, z) \\ g'(z) = \begin{cases} 0.01 &\text{if } z<0 \\ 1 &\text{if } z>0 \\ undefined &\text{if } z=0 \end{cases}\)
为什么需要一个非线性的激活函数(Non-linear Activation Function)
因为如果是线性的, 即直接令 \(A = g(Z) = Z\) 那么对于每一层,都有: \[ a^{[i]} = z^{[i]} = w^{[i]}a^{[i-1]} + b^{[i]} \tag{*} \]
则对于第 \(i+1\) 层, 将 \((*)\) 带入:
\[ \begin{aligned} a^{[i+1]} & = z^{[i+1]} \\ & = w^{[i+1]}a^{[i]} + b^{[i+1]} \\ & = w^{[i+1]}(w^{[i]}a^{[i-1]} + b^{[i]} + b^{[i+1]} \\ & = (w^{[i+1]}w^{[i]})a^{[i-1]} + (w^{[i+1]}b^{[i]}+b^{[i+1]}) \\ & = w'a^{[i-1]} + b' \end{aligned} \]
即最终的模型相当于一个标准的, 没有隐藏层的逻辑回归. 即无论你的模型有多少层,最终效果也相当于只有一层。
如果要用线性激活函数, 一般也只用在回归问题的输出层(预测一些结果为实数的值), 隐藏层还是用 tanh, ReLU 等.
为什么神经网络要随机初始化参数(而逻辑回归不须要)
如果神经网络不随机初始化, 比如 w, b 都初始化为0, 则每次对隐藏层反向传播的时候计算得的导数 \(dz^{[i]}_1\) , \(dz^{[i]}_2\) , \(dz^{[i]}_3\) 等相同, \(dw\) 也是, 每个隐藏层单元都计算着一模一样的式子(不过b不受这种Symmetry Breaking Problem影响, 可以初始化为0).
而对于逻辑回归, 它没有隐藏层, 其导数取决于x, 问题不大.
随机初始化时参数范围可以设置在0~0.01(对于 sigmoid 和 tanh 而言), 如果参数过大(比如w=100) 在 sigmoid 或 tanh 的函数图像上可以看到参数十分靠右,导致导数趋于零, 梯度趋于零, 导致收敛很慢.
向前向后传播
向前传播:
\[ \begin{aligned} & \text{Input: } a^{[l-1]} \\ & \text{Output: } a^{[l]} , \text{Cache: } z^{[l]} \\ & z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]} && Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]} \\ & a^{[l]} = g^{[l]}(z^{[l]}) && A^{[l]} = g^{[l]}(Z^{[l]}) \\ \end{aligned} \]
向后传播:
\[ \begin{aligned} & \text{Input: } da^{[l]} \\ & \text{Output: } da^{[l-1]} , dW^{[l]} , db^{[l]} \\ & dz^{[l]} = da^{[l]}*g^{[l]'}(z^{[l]}) && dZ^{[l]} = dA^{[l]}*g^{[l]'}(Z^{[l]}) \\ & dW^{[l]} = dz^{[l]}a^{[l-1]} && dW^{[l]} = \frac{1}{m} dZ^{[l]}A^{[l-1]^T} \\ & db^{[l]} = dz^{[l]} && db^{[l]} = \frac{1}{m} np.sum(dZ^{[l]}, axis=1, keepdims=True) \\ & da^{[l-1]} = w^{[l]^T}dz^{[l]} && dA^{[l-1]} = W^{[l]^T}dZ^{[l]} \end{aligned} \]