概念与表述
线性回归与逻辑回归的缺点:特征太多的时候计算负荷太大。
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。 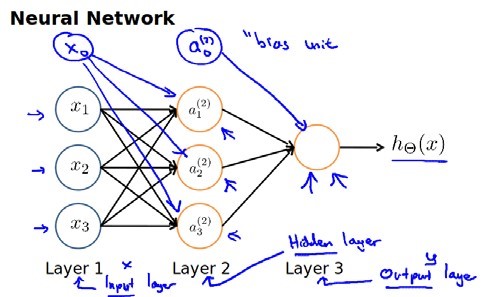
直观理解
神经网络的单层神经元的计算可以用来表示逻辑运算,比如AND、OR。
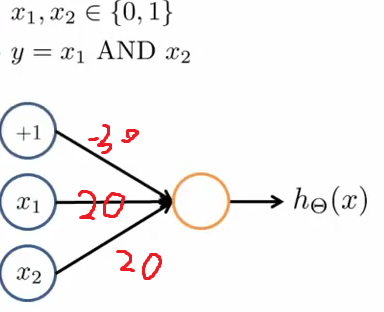


如果用多层的话就可以组成功能复杂的神经网络。

多类分类
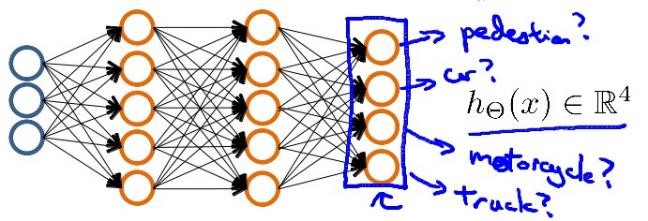
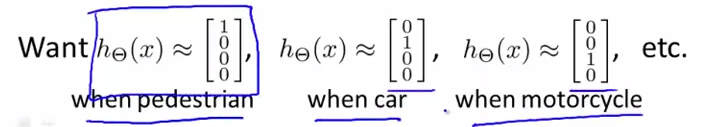
代价函数
逻辑回归的代价函数:
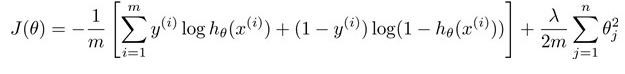
神经网络代价函数:(\(h_{\theta}(x)\)为K维度的向量,因为神经网络中可以输出很多变量。训练集中的因变量也是K维度)

反向传播算法
预测结果时我们正向传播:从第一层正向一层层传播,直到最后一层\(h_{\theta}(x)\) 。
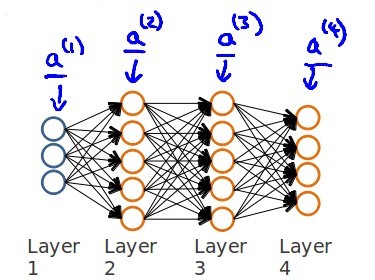
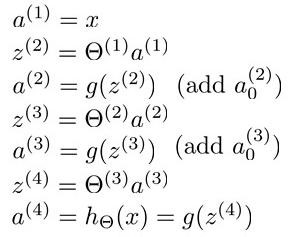
计算代价函数的偏导数时,从最后一层的误差算起,一层层反向求出各层误差,直到倒数第二层。设误差为\(\delta\) :
\(\delta^{(n)}=a^{(n)}-y\) \(\delta^{(n-1)}=(\theta^{(n-1)})^{T}\delta^{(n)}.*g'(z^{(n-1)})\) \(...\) \(\delta^{(2)}=(\theta^{(2)})^{T}\delta^{(3)}.*g'(z^{(2)})\)
于是偏导数的表达式即为:$ J()=a_{ij}^{(l)}_{i}^{l+1}$ 。
l代表目前所计算的是第几层。 j代表目前计算层中的激活单元(神经元)的下标,也将是下一层的第j个输入变量的下标。 i代表下一层中误差单元的下标,是受到权重矩阵中第i行影响的下一层中的误差单元的下标。
步骤总结
参数的随机初始化
利用正向传播方法计算所有的hθ(x)
编写计算代价函数J的代码
利用反向传播方法计算所有偏导数
利用数值检验方法检验这些偏导数
使用优化算法来最小化代价函数